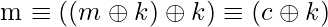Super lightweight encryption lib

FFP cypher is totally insecure and naive, use for educational purposes only 💖

index

• RSA (for asymmetric encryption)
• XOR (for symmetric encryption)
• hacha (simple SDBM hash function with reasonable entropy)
• requiresWork (string, difficulty)
• proofOfWork (string, hash, nonce)

usage

• asymmetric encryption

  //
  // one step
  const rsa = require('../src/RSAKeys');
  const keys = rsa.generateKeys(512);
  //Generated Random public key,
  //jb1yruw21v4t0am0tr0msy5iam07oawertgg6joo48vtm30hanf1fabmjnlxnvupcene6qyg836512blu
  //cnacq9dja0hght517y5n90iag8izipy1w8hf4ot62bos6vn9o5nn1ygmqgjhuss3xqp9w0b86alrks2c9
  //5xu9s9ihqf38atrd5r0b6szknf3eronmno1d/qjbiu8xs0msnk88sfh4dhb7va71p7xssw2u4e9b8ijqoh3avh
  //-------------------------------------------
  //Generated private key,
  //ha3mn77xg0dzm1g53xtirzwlnr2kjgrdjcpqlk1dley8s2ulwp6tyd0eryvn9m619eth4fjygntg4cu7ju
  //7fi3c5ek1grizehjyxplq4ui1mk8pykegf7fx4nojeay9nvrhjvamepw1bzt88durduvmvr5500qaxv6s
  //znx4wpzm7uroe0r6qzq44e4djnudjwh8xpt
  //-------------------------------------------


  // encryption
  const RSA = require('../src/RSA').RSA;
  const $rsa = new RSA(keys.bits);

  const cypher = $rsa.encrypt("olivier!",keys.publicKey);
  const message = $rsa.decrypt(cypher,keys.publicKey,keys.privateKey);

• symmetric encryption

  const XOR = require('../src/XOR');
  const xor = new XOR();
  const cypher = xor.encrypt("olivier!",'privatekey');
  const message = xor.decrypt(cypher,'privatekey');

• proof of work

  const requiresWork = require('../src/utils').requiresWork;
  const proofOfWork = require('../src/utils').proofOfWork;

    const string = 'Olivier is learning something here';
    //
    // CPU difficulty lower => 0x4fffn or higher => 0x8fffn, or 0xffffn 
    const difficulty = 0x6fffn; // ~400ms on my computer
    const work = requiresWork(string,difficulty);
    
    //
    // verify proof
    proofOfWork(string,work[0],work[1]).should.equal(true);

• hacha

  const hacha = require('../src/utils').hacha;
  //
  // convert string to 128bits BigInt with reasonable entropy and poor collision
  const hex = hacha('oliviertest');
  hex.toString(16).should.equal('57a8eb282a383a5ec');

Documentation

Entropy

• http://www.russellcottrell.com/mousePointerRNG.htm
• https://pomcor.com/2018/07/04/random-bit-generation-with-full-entropy-and-configurable-prediction-resistance-in-a-node-js-application/
• https://github.com/usnistgov/SP800-90B_EntropyAssessment

Math behind Hash functions

• Pre-Image Resistance,
  • it should be computationally hard to reverse a hash function!
  • it should be hard to find a different input with the same hash!
  • it should be hard to find two different inputs of any length that result in the same hash( collision)!
• https://en.wikipedia.org/wiki/Cryptographic_hash_function
• https://www.partow.net/programming/hashfunctions/#SDBMHashFunction

relatively Prime

• e is relatively Prime of a if PGCD(e,a) = 1

modular inverse

If a aa and NNN are integers such that gcd⁡(a,N)=1, then there exists an integer x xx such that ax≡1(modN).

• x≡a⁻¹ (mod N)
• (a * X) % N = 1

Modulo operation

• a² % n = [(a mod n)²] mod n.
• (a + b) mod n = [(a mod n) + (b mod n)] mod n.
• ab mod n = [(a mod n)(b mod n)] mod n.
• https://en.wikipedia.org/wiki/Modulo_operation#Properties_(identities)

Modular exponentiation

• a^e % m (HAC 14.85)
• https://en.wikipedia.org/wiki/Modular_exponentiation#Pseudocode

Our HaHaCha

• forEach((hash << 6n) + (hash << 16n) + BigInt(char.charCodeAt(0)) - hash);
• https://www.desmos.com/calculator/hdlcacu5uj

Simple RSA (asymmetric)

• https://brilliant.org/wiki/rsa-encryption/

• Half of the public key N=pq, e = seed

• compute the encrypted message, c ≡ m^e(mod N)

• compute the original message c^d ≡ m (mod N)

XOR cypher (symmetric)

Let m be a plaintext message, k be the encryption key, and c be the encrypted message.

• source The making of the XOR cipher

Notes

• a^x % n (HAC 14.79) (HAC 14.85)
• x = x/R mod m (HAC 14.32)
• https://gist.github.com/jimklo/3036199#file-openpgp-js-L171